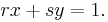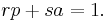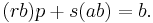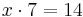Euclid's lemma
In mathematics, Euclid's lemma (Greek λῆμμα) is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers. This key fact requires a surprisingly sophisticated proof (using Bézout's identity), and is a necessary step in the standard proof of the fundamental theorem of arithmetic.
Euclid's lemma (also known as Euclid's first theorem) appears as proposition 30 in Book VII of Euclid's Elements. In modern notation:
- If
is prime and 
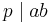then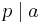 
and/or 
.
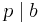Here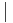 
means “divides”; that is, 
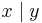if 
is a divisor of 
.
In modern mathematics, “Euclid's lemma” is often used to refer to the following generalization of this statement:
- If
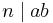and 
and 
are relatively prime, then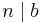 
.
This statement reduces to Euclid's proposition 30 in the case where is prime.
The standard proof of Euclid's lemma uses Bézout's identity. This states that, for any relatively prime integers x and y, there exist integers r and s such that
To prove Euclid's lemma, suppose that p is a prime factor of ab, but that p is not a factor of a. Then p and a must be relatively prime, so there exist integers r and s such that
Multiplying through by b gives
Now, the first term on the left is clearly a multiple of p. Since p divides ab, the second term on the left hand side of the equation is also a multiple of p. It follows that b is a multiple of p, so p divides b. This proves that p is always either a divisor of a, a divisor of b, or both. Q.E.D.[1]
Alternate proof without Bézout's identity
This proof does not use Bézout's identity, or even Euclidean division.
We wish to prove the following statement for any nonnegative integers p, a and b, with p prime (and positive):
(*) if p divides ab, then p divides a and/or p divides b.
In order to achieve a contradiction, assume the theorem is false. Then there is some smallest prime number p as above for which there are a and b making (*) false. That is, p divides ab but divides neither a nor b. For this choice of p, pick a and b making (*) false, with a as small as possible.
Note that since we choose a and p as small as possible, the theorem (*) has to be true for all smaller numbers. This fact will be used in this proof.
First we see that a > 1. If a = 0, then p divides a, making (*) true, a contradiction. If a = 1, then ab = b. Since p divides ab by assumption, it also divides b, again contradicting the choice of a and b. Therefore a > 1.
Next we prove a is prime. Otherwise, we could write a = cd, with 1 < c,d < a. Since c < a, and a was chosen as small as possible, (*) is true for the numbers p, a′ and b′, where a′ = c and b′ = db. Now p divides ab = cdb, so by (*), p either divides c or divides db. If p divided c, it would also divide cd = a, contradicting the choice of a. Therefore p divides db. Since d < a, we may again apply (*) to conclude that p either divides d or divides b. p does not divide b, by hypothesis. But again, if p divided d, it would also divide cd = a, contradicting the choice of a. Thus the assumption that a was not prime was impossible.
Now we prove that a < p. Otherwise, write a′ = a - p ≥ 0. Then a′b = (a - p)b = ab - pb. Since p divides ab by hypothesis, and clearly also divides pb, it must divide their difference, which is a′b. Since a′ < a, and a was chosen as small as possible, (*) must be true for p, a′ and b. Therefore p divides a′ and/or p divides b. But since by assumption p does not divide b, p must divide a′. Therefore p divides a′ + p = a, a contradiction.
Since a is prime, a < p, and p was the smallest prime number for which the theorem was false, we conclude that the theorem is true for a. That is, if a divides any product cd, then it divides one of the factors c or d.
Now since p divides ab, we can write ab = cp for some number c. This shows that a divides cp. Since the theorem is true for a, either a divides c or a divides p. But a cannot divide p, since p is prime and 1 < a < p. Therefore a divides c, so we can write c = ak for some k. Thus ab = cp = akp. Hence, dividing by a, we find b = kp, whence p divides b, contradicting the choice of b. This shows that the theorem is true for p, contradicting the choice of p. In conclusion, the theorem must be true.
Example
Euclid's lemma in plain language says: If a number N is a multiple of a prime number p, and N = a · b, then at least one of a and b must be a multiple of p. Say,
,
,
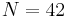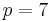and
.
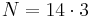Then either
or
.
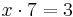Obviously, in this case, 7 divides 14 (x = 2).